Paper
https://arxiv.org/abs/2009.07842
Please cite as:
@misc{ashutosh2020lower,
title={Lower Bounds for Policy Iteration on Multi-action MDPs},
author={Kumar Ashutosh and Sarthak Consul and Bhishma Dedhia and Parthasarathi Khirwadkar and Sahil Shah and Shivaram Kalyanakrishnan},
year={2020},
eprint={2009.07842},
archivePrefix={arXiv},
primaryClass={cs.LG}
}
Motivation
We took this problem initially as part of an elective course CS 747 - Fundamentals of Intelligent and Learning Agents and later continued working on the problem and eventually submitted to IEEE CDC 2020. The project was interesting because it involved rigorous understanding of both MDP and Policy Iterations. We came up with several hypothesis and then spent time verifying them through simulations and theoretical proofs. We came up with Lower Bounds for several versions of Policy Iterations. Firstly, we showed the lower bound for generic n-state, k-action Simple PI. Subsequently, we extended the construction to accomodate Randomized PI followed by Howard PI (two variations) and finally devised a policy iteration algorithm which has a very strong lower bounds. Each of them is described in subsequent sections.
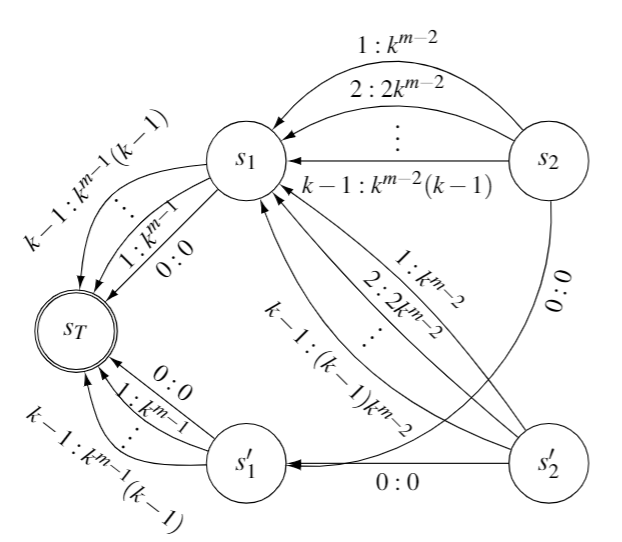
Simple Policy Iteration
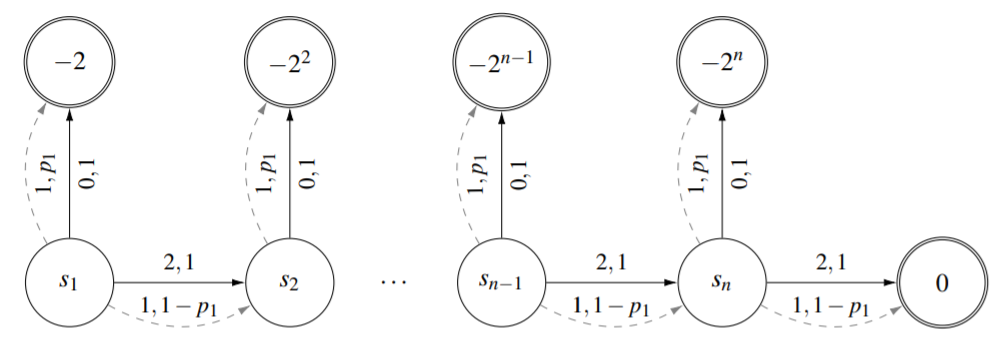
An earlier work by Melekopoglou and Condon showed a lower bound of $2^(n-1)$ for a n-state 2-action MDP. We drew motivation from that MDP and tried coming up with extensions show that the lower bound if multiplicative in the number of actions. This is particularly challenging because we need to maintain a strict order of Value functions in order make the algorithm traverse a lot of states. In addition, the number of parameters here is also high and using a for loop to come up with such MDP is infeasible.
The MDP above takes O(k.2^n) iterations starting from an all 0 state. Setting n=2 and epsilon=0 gives back the construction shown by Melekopoglou and Condon. We show through simulations and proofs that there are feasible values of epsilon (for eg. 2^(-n)) such that all the constraints are satisfied. This MDP also has the advantage that it is easy to incorporate random action selection in this MDP. The resulting lower bound is O(log(k) 2^n). Detailed proof and simulation is available in the paper and the github repository, respectively.
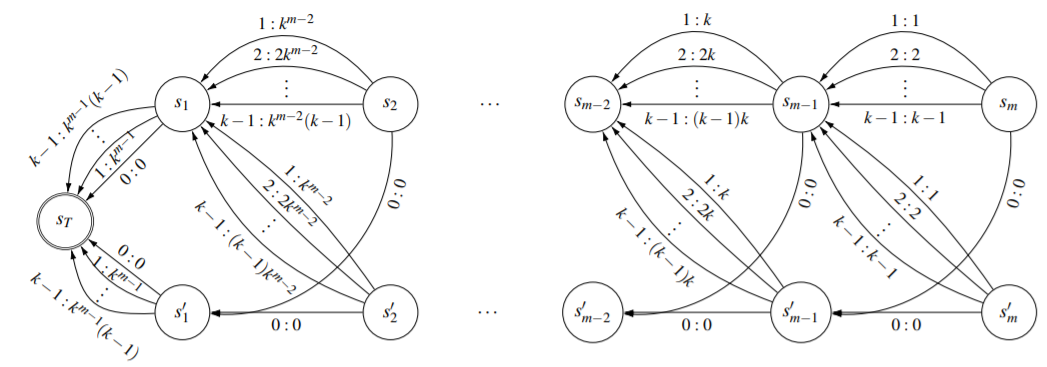
Howard’s Policy Iteration
After establishing lower bounds for Simple PI, we turned our focus to more sophisticated Howard PI. As per the Howard PI, “all” the improvable states are switched. In this construction, we assume the chosen action is heuristic and not based on Q matrix. For this part, we took inspiration from a similar work done to minimize the mean cost cycle for directed graphs by Hansen and Zwick. The final construction is much simpler than the construction proposed by them.
In this construction we ensure that at any point, only one state is improvable at a time. This constraint ensures that the policy trajectory is such that a maximum number of states are traversed. Again, a randomized version of this PI is simple and the corresponding lower bound is O(log(k) n) compared to O(kn) for deterministic Howard PI.
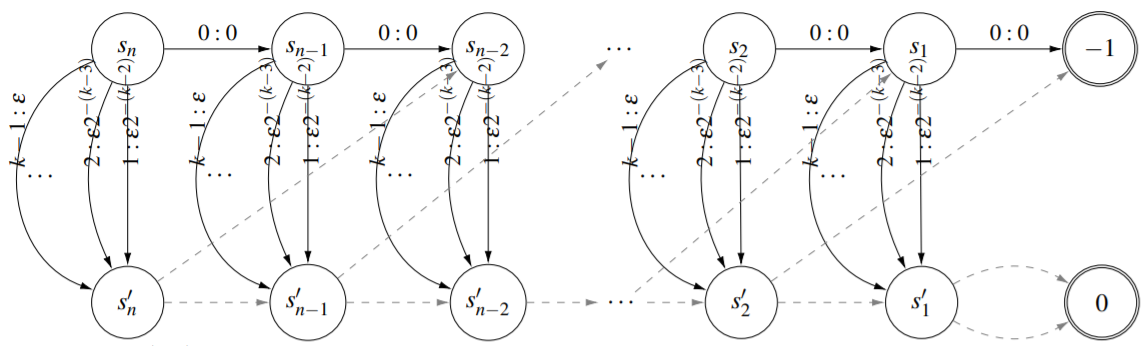
Trajectory of O(k^(0.5n))
Any PI will have a trivial upper bound of k^n. The aim of the study of lower bounds is to tighten this gap between lower and upper bounds. Next, we try to tighten this gap by proposing a family of MDP and PI to achieve a lower bound of O(k^(0.5n)). The basic idea is to make the transition traverse all possible combinations of exactly (n/2) states. There are (n/2) additional states which we call as “dummy states”. Therefore the lower bound is of the order O(k^(0.5n)) which is a very strong lower bound considering the trivial upper bound of k^n.
Conclusion
Through this work, we have tightened the gap between the lower bound and the upper bound. The study of lower bound is particulary crucial in understanding the “worst-case” performance of an algorithm. Future work includes finding similar lower bounds for more sophisticated Policy Iteration algorithms and further tightening the gap between the lower and the upper bounds.
Acknowledgement
I thank Professor Shivaram for his constant guidance and help throughout the ideation stage and paper-writing stage. Lastly, thankful to all the co-authors - Sarthak, Bhishma, Parth and Sahil. We did it guys!